SOAL TRANSFORMASI DAN PENYELESAIANNYA
Translasi merupakan pergeseran atau pemindahan semua titik pada bidang geometri sejauh dan arah yang sama. Penulisan atau notasi translasi sama dengan notasi vektor. Jika titik B ditranslasi sampai titik maka dapat dinotasikan:
Sebagai contoh:

Titik A, B, dan C, masing-masing ditranslasikan ke titik AI, BI, dan CI dengan jarak dan arah yang sama.
Suatu translasi dapat ditinjau terhadap sumbu x dan sumbu y. Pergeseran sejauh a sejajar sumbu x (bergeser ke kanan a>0, ke kiri a<0) dan pergeseran sejauh b sejajar sumbu y (bergeser ke atas b>0, ke bawah b<0) dinyatakan sebagai:
Dengan a dan b adalah komponen translasi. Bentuk-bentuk translasi sejauh sebagai berikut:
Refleksi
Refleksi merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri kearah sebuah garis atau cermin dengan jarak sama dengan dua kali jarak titik kecermin. Ada dua sifat penting dalam refleksi:
- Jarak titik kecermin sama dengan jarak bayangan titik ke cermin.
- Geometri yang direfleksikan berhadapan dengan petanya.
Sebagai contoh:

Selain refleksi terhadap garis diatas, titik dan kurva juga dapat direfleksikan terhadap suatu garis y=mx+k. Berikut refleksinya:


Rotasi
Rotasi atau perputaran merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri sepanjang busur lingkaran yang memiliki titik pusat lingkaran sebagai titik rotasi. Rotasi dinyatakan positif jika arahnya berlawanan jarum jam, dan bernilai negatif jika searah jarum jam. Sebagai contoh:

Titik A berotasi 90o berlawanan arah jarum jam. Dalam diagram cartesius, bentuk-bentuk rotasi sebagai berikut:

Dilatasi
Dilatasi merupakan transformasi geometri berupa perkalian yang memperbesar atau memperkecil suatu bangunan geometri. Dalam konsep dilatasi, ada yang disebut titik dilatasi dan faktor dilatasi.
Titik dilatasi merupakan titik yang menentukan posisi suatu dilatasi. Titik dilatasi menjadi titik pertemuan dari semua garis lurus menghubungkan antara titik-titik dalam suatu bangun ketitik-titik hasil dilatasi.
Dilatasi dapat ditulis:
(D, k) = (Titik dilatasi, faktor dilatasi)
Konsep dilatasinya:
Dengan ketentuan:
- k adalah titik dilatasi
- A salah satu titik geometri
- AI hasil dilatasi titik A
Dalam diagram cartesius, bentuk-bentuk rotasi sebagai berikut:

Matriks Transformasi
Secara umum, transformasi geometri dapat dinyatakan dalam bentuk matriks yang memetakan titik (x,y) ke titik (x’,y’ ) dengan persamaan:
Atau
Bentuk-bentuk matriks transformasi sebagai berikut:

Determinan dan Luas
Hasil transformasi bangun geometri memiliki luas yang berbeda dengan bangun awalnya. Untuk mendapatkan luas dari sebuah bangun geometri yang telah ditransformasi dapat dicari dengan determinan matriks transformasi. Yaitu:
Luas
Dengan dan diketahui luas awalnya.
SOAL DAN PEMBAHASAN
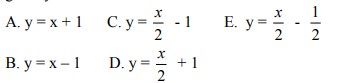
Jawaban : C
Pembahasan :

2. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah ….
B. y = x² – 2x + 3
C. y = x² + 2x + 3
D. x = y² – 2y – 3
E. x = y² + 2y + 3
Jawaban : D
Pembahasan :
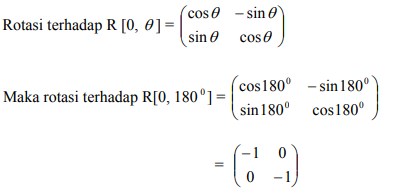
Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.
pencerminan terhadap garis y = -x

![]() adalah….
adalah….
A. x² + y² – 6x – 4y- 3 = 0
B. X² + y² – 6x + 4y- 3 = 0
C. x² + y² + 6x – 4y- 3 = 0
D. x² + y² – 4x + 6y- 3 = 0
E. x² + y² + 4x – 6y+ 3 = 0
Jawaban : A
Pembahasan :

4. T1 dan T2 adalah transformasi yang masing-masing bersesuaian dengan
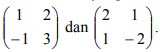 Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…
Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…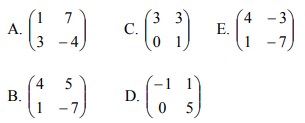
Jawaban : E
Pembahasan :

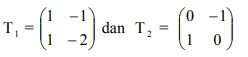 Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah….
Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah….
A. (-4,3)
B. (-3,4)
C. (3,4)
D. (4,3)
E. (3,-4)
Jawaban : A
Pembahasan :

6. Persamaan bayangan garis y = -6x + 3 karena transformasi oleh matriks
![]() kemudian dilanjutkan dengan matriks
kemudian dilanjutkan dengan matriks 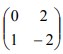 adalah…
adalah…
A. x + 2y + 3 = 0
B. x + 2y – 3 = 0
C. 8x – 19y + 3 = 0
D. 13x + 11y + 9 = 0
E. 13x + 11y – 9 = 0
Jawaban : E
Pembahasan :








Komentar
Posting Komentar