INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

Assalamualaikum wr,wb

Hello everyone!!! Ketemu lagi dengan saya Naila Mutiara Ziefa XI IPS 2.

jadi,diblog saya kali ini,saya akan membahas tentang INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

Integral adalah suatu bentuk pada operasi matematika yang menjadi kebalikan atau biasa juga disebut sebagai invers dari operasi turunan. Serta limit dari jumlah maupun suatu luas daerah tertentu.

Integral tak tentu (bahasa Inggris: indefinite integral) atau antiderivatif adalah suatu bentuk operasi pengintegralan suatu fungsi yang menghasilkan suatu fungsi baru. Fungsi ini belum memiliki nilai pasti (berupa variabel) sehingga cara pengintegralan yang menghasilkan fungsi tak tentu ini disebut “integral tak tentu”.

• Cara Membaca Integral Tak Tentu

Setelah membaca uraian di atas, taukah kalian cara membaca kalimat integral? Integral di baca seperti ini:

yang di baca Integral Tak Tentu Dari Fungsi f(x) Terhadap Variabel X.

Rumus Umum Integral

Berikut ini adalah rumus umum yang ada pada integral:

• Pengembangan Rumus Integral

Mari perthatikan baik-baik contoh dari beberapa turunan dalam fungsi aljabar di bawah ini:

Sifat Integral

Sifat-sifat dari integral antara lain:

• ∫ k . f(x)dx = k. ∫ f(x)dx                         (dengan k adalah konstanta)
• ∫ f(x) + g(x)dx = ∫ (x)dx + ∫ g(x)dx
• ∫ f(x) – g(x)dx = ∫ f(x)dx – ∫ g(x)dx

Menentukan Persamaan Kurva

Gradien serta persamaan garis singgung kurva pada suatu titik.

Apabila y = f(x), gradien garis singgung kurva pada sembarang titik pada kurva adalah y’ = = f'(x).

Oleh karena itu, apabila gradien garis singgungnya telah diketahui sehingga persamaan kurvanya dapat ditentukan dengan cara seperti berikut ini:

y = ∫ f ‘ (x) dx = f(x) + c

Jika salah satu titik yang melewati kurva telah diketahui, nilai c dapat juga diketahui sehingga persamaan kurvanya dapat ditentukan.

Contoh Soal Integral

No.1

Pembahasan

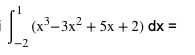
Dalam soal ini, batas atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah melakukan integral fungsi  3x2 + 5x + 2 menjadi seperti di bawah ini.

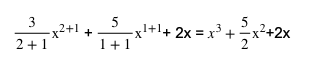
Setelah kita mendapatkan bentuk integral dari fungsi tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut lalu mengurangkannya menjadi seperti berikut.

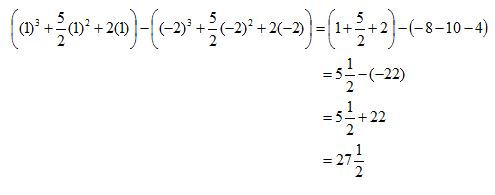
Hasil dari integral tersebut adalah 27,5.

No.2

Diketahui turunan y = f(x) adalah = f ‘(x) = 2x + 3

Jika kurva y = f(x) lewat titik (1, 6), maka tentukan persamaan kurva tersebut.

Jawab:

f ‘(x) = 2x + 3.
y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.

Kurva melalui titik (1, 6), berarti f(1) = 6 hingga dapat di tentukan nilai c, yakni 1 + 3 + c = 6 ↔ c = 2.

Maka, persamaan kurva yang dimaksud yaitu:

y = f(x) = x2 + 3x + 2.

No.3

Carilah hasil dari ʃ21 6x2 dx !

Pembahasan

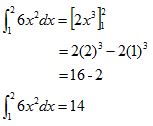
Jadi, hasil dari ʃ21 6x2 dx adalah 14.

No.4

Gradien garis singgung kurva pada titik (x, y) ialah 2x – 7. Apabila kurva itu melewati titik (4, –2), maka tentukanlah persamaan kurvanya.

Jawab:

f ‘(x) = = 2x – 7
y = f(x) = ʃ (2x – 7) dx = x2 – 7x + c.

Sebab kurva melewati titik (4, –2)
maka:

f(4) = –2 ↔ 42 – 7(4) + c = –2
–12 + c = –2
c = 10

Maka, persamaan kurva tersebut yakni:

y = x2 – 7x + 10.

Berapakah nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx ?

Pembahasan

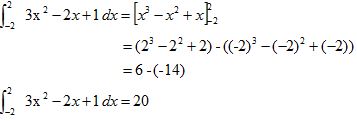
Jadi, nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx adalah 20.

No.5

Hitunglah nilai integral tentu dari ʃ⁹₄ 1/√x dx !

Pembahasan

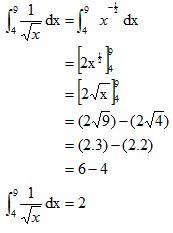
Jadi, nilai integral tentu dari ʃ⁹₄ 1/√x dx adalah 2.

DAFTAR PUSTAKA:

https://www.seputarpengetahuan.co.id/2020/05/integral-tak-tentu.html