Assalamualaikum wr,wb
Hello everyone!!! Ketemu lagi dengan saya Naila Mutiara Ziefa XI IPS 2.
jadi,diblog saya kali ini,saya akan membahas tentang Soal Kontekstual Yang Berhubungan Dengan Turunan.
Soal 1
Suatu perusahaan memproduksi x unit barang dengan biaya (4x2−8x+24) ribu rupiah untuk tiap unit. Jika barang tersebut terjual habis dengan harga Rp40.000,00 untuk tiap unit, maka keuntungan maksimum yang diperoleh perusahaan tersebut adalah...
A. Rp16.000,00 D. Rp52.000,00
B. Rp32.000,00 E. Rp64.000,00
C. Rp48.000,00
Pembahasan:
Misalkan f(x) menyatakan total biaya produksi x unit barang, g(x) menyatakan harga jual x unit barang dalam satuan ribu rupiah, dan h(x) menyatakan keuntungan yang diperoleh atas penjualan x unit barang, maka
f(x) =x (4x² − 8x + 24)
=4x³ − 8x² + 24x
g(x)=40x
h(x)=g(x)−f(x)
=40x − (4x³ − 8x² + 24x)
=−4x³ + 8x² +16x
Agar maksimum, nilai turunan pertama h′(x) harus bernilai 0.
h(x)=−4x³ + 8x² + 16x
h'(x)=−12x² + 16x +16
0 =−12x² + 16x + 16
Bagi kedua ruas dengan -4
0 = 3x² − 4x − 4
0 = (3x + 2)(x − 2)
Diperoleh x = - 2/3 atau x = 2 karena x.
menyatakan jumlah barang dan nilainya tidak mungkin negatif/pecahan, maka x yang diambil adalah x = 2.
Substitusikan x = 2 ke h.
h(2)= −4(2)³ + 8(2)² + 16(2)
= −4(8) + 8(4) + 32 =32
Jadi, keuntungan maksimum yang diperoleh perusahaan tersebut adalah Rp32.000,00.
(Jawaban B)
Soal 2
Sebuah peluru ditembakkan ke atas. Jika tinggi h meter setelah t detik dirumuskan dengan h(t)=120t − 5t² ,maka tinggi maksimum yang dicapai peluru tersebut adalah... meter.
A. 270 C. 670 E. 770
B. 320 D. 720
Pembahasan
Diketahui: h(t)=120t − 5t².
Turunan pertama fungsi h adalah
h′(t)=120 − 10t
Nilai t akan maksimum saat h′(t)=0, sehingga ditulis
120 – 10t =0⇔10t =120⇔t =12
Ketinggian maksimum yang dapat dicapai peluru adalah saat t=12, yaitu
h(12)= 120(12) − 5(12)²
=1440−720 =720
Jadi, ketinggian maksimum peluru adalah 720 meter.
(Jawaban D)
Soal 3
Sebuah benda dilemparkan keatas dengan persamaan gerak
Soal 4
Turunan pertama dari
=\frac{2}{3}x^3+3x^2-5x+10)
adalah ...
A. x² + 3x - 5
B. 2x² + x - 5
C. 2x + 3x - 5
D. 2x + 6x - 5
E. 2x + 6x + 5
Pembahasan :
=\frac{2}{3}.3x^{3-1}+3.2x^{2-1}-5.1x^{1-1})
=2x^2+6x-5)
(Jawaban D)
Soal 5
Untuk memproduksi x unit pakaian dalam satu hari diperlukan biaya produksi (x2+4x−10) ratus ribu rupiah. Harga jual pakaian itu tiap unitnya adalah (20−x) ratus ribu rupiah. Keuntungan maksimum yang dapat diperoleh setiap harinya adalah...
A. Rp1.200.000,00 D. Rp2.000.000,00
B. Rp1.500.000,00 E. Rp2.200.000,00
C. Rp1.800.000,00
Pembahasan:
Misalkan keuntungan (U) dianggap sebagai fungsi terhadap variabel x (ingat bahwa keuntungan didapat dengan mengurangi harga jual terhadap pengeluaran/biaya produksi), sehingga
U(x)=x(20 − x) − (x² +4x +10)
=20x − x² − x² − 4x + 10
=−2x² + 16x −10
Keuntungan akan maksimum apabila
U′(x) =0
U′(x) =0
−4x + 16 =0
4x = 16
x = 4
Keuntungan maksimum tercapai saat memproduksi 4 unit pakaian, yaitu
U(4) = −2(4)² + 16(4) − 10
= -32 + 64 − 10 =22
Jadi, keuntungan maksimum yang dapat diperoleh setiap harinya adalah Rp2.200.000,00.
(Jawaban E)
Soal 6
Dari selembar karton berbentuk persegi yang panjang sisinya 30 cm akan dibuat kotak tanpa tutup dengan cara menggunting empat persegi kecil di setiap pojok karton seperti gambar.

Volume kotak terbesar yang dapat dibuat adalah...cm³.
A. 2.000 D. 5.000
B. 3.000 E. 6.000
C. 4.000
Pembahasan:
Misalkan panjang sisi persegi kecil adalah x cm (akan menjadi tinggi kotak) sehingga panjang dan lebar balok menjadi (30−2x) cm. Perhatikan juga bahwa interval nilai x yang mungkin adalah 0<x<15.
Nyatakan volume kotak/balok (V) sebagai fungsi terhadap variabel x.
V(x)= plt
=(30−2x) (30−2x)x
=4x³ − 120x² + 900x
Volume kotak akan maksimum apabila
V′(x)=0
V′(x)=0
12x² − 240x + 900 =0
Bagi kedua ruas dengan 12
x² − 20x + 75 =0
(x−15) (x−5) =0
Diperoleh x=15 (tidak memenuhi) atau x=5.
Untuk x=5, diperoleh
V(5)= 900(5) − 120(5)² + 4(5)³
=4.500 − 3.000 + 500
=2.000
Jadi, volume kotak terbesar yang dapat dibuat adalah 2.000 cm³
(Jawaban A)
Soal 7
Persamaan garis singgung pada kurva  dititik yang mempunyai absis
dititik yang mempunyai absis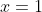 adalah...
adalah...
A. y = 4 - 2x
B. y = 6 - 2x
C. y = 2x + 7
D. y = 2x + 10
E. y = 2x + 11
Pembahasan:
Untuk 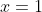 ,
, ^2+3(1)+7&space;=&space;9)
titik singgung garis di ;x_{1}=1) dan
dan  .
.
Gradien garis singgung

untuk ^2-4(1)+3=2)
Jadi, persamaan garis mempunyai gradien 2 dan melalui titik ) adalah
adalah
)
)
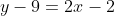
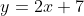 (Jawaban C)
(Jawaban C)
Soal 8
Sebuah peluru ditembakan vertikal keatas. Tinggi peluruh (h) dalam meter dengan waktu (t) dalam sekon dinyatakan dengan =21t-6t^2.) Waktu untuk mencapai tinggi maksimum adalah ...
Waktu untuk mencapai tinggi maksimum adalah ...
A. 1 sekon
B. 1,25 sekon
C. 1,5 sekon
D. 1,75 sekon
E. 2 sekon
Pembahasan :
=21t-6t^2) untuk menentukan maksimum/minimum, maka:
untuk menentukan maksimum/minimum, maka:
=0)
=21-12t)

 Jadi, waktu maksimum untuk mencapai ketinggian adalah 1,75 sekon
Jadi, waktu maksimum untuk mencapai ketinggian adalah 1,75 sekon
(JAWABAN: D)
Daftar Pustaka:
https://mathcyber1997.com/soal-dan-pembahasan-aplikasi-turunan-diferensial/
https://kingmathematic.blogspot.com/2019/03/soal-cerita-materi-turunan.html



Komentar
Posting Komentar